Hỏi đáp online nhanh chóng, chính xác và hoàn toàn miễn phí
Toán Học - L9 - 01/03/2024 08:25:04
Cho tam giác ABC vuông tại A, đường cao AH.
a) Giải tam giác vuông biết
b) Đường thẳng vuông góc với BC tại B cắt tia CA tại K. Kẻ AE vuông góc với BK (E∈BK)
. Chứng minh
c) Gọi M là trung điểm của cạnh AC. Kẻ MN vuông góc với BC tại N. Chứng minh AN=BM.cosC
reply 01/03/2024 08:25:04
Hướng dẫn giải
a) Vận dụng các kiến thức về hệ thức lượng và định lí Pythagore trong tam giác vuông để giải tam giác.
b) Chứng minh AHBE là hình chữ nhật nên AB = HE.
Chứng minh ΔABK đồng dạng ΔBCK(g.g) suy ra . Từ đó chứng minh được . c) Chứng minh ΔABC đồng dạng ΔNMC(g.g) suy ra . Chứng minh ΔBMC dong dang ΔANC(c.g.c) suy ra . Biểu diễn cosC trong tam giác vuông ABC. Từ đó suy ra điều phải chứng minh.
Hướng dẫn giải
a) Vận dụng các kiến thức về hệ thức lượng và định lí Pythagore trong tam giác vuông để giải tam giác.
b) Chứng minh AHBE là hình chữ nhật nên AB = HE.
Chứng minh ΔABK đồng dạng ΔBCK(g.g) suy ra . Từ đó chứng minh được . c) Chứng minh ΔABC đồng dạng ΔNMC(g.g) suy ra . Chứng minh ΔBMC dong dang ΔANC(c.g.c) suy ra . Biểu diễn cosC trong tam giác vuông ABC. Từ đó suy ra điều phải chứng minh.
reply 01/03/2024 08:25:04
Xin cho biết cách giải chi tiết hơn ?
Xin cho biết cách giải chi tiết hơn ?
reply 01/03/2024 08:25:04
Chi tiết:
a) Xét tam giác ABC vuông tại A, số đo góc B là: Áp dụng tỉ số lượng giác trong tam giác vuông vào tam giác ABC, ta có: Suy ra
Áp dụng định lí Pythagore vào tam giác vuông, ta có:
= 24 (cm).
Vậy là ta đã có góc B, cạnh AC và cạnh BC.
b) Xét tứ giác AHBE có: (=90 độ) nên tứ giác AHBE là hình chữ nhật, suy ra AB = HE. (1)
Xét tam giác ABK và tam giác ACB có:
ˆBAK= ˆCAB(=90∘)
ˆAKB=ˆABC(cùng phụ với ˆC)
suy ra ΔABK đồng dạng ΔBCK(g.g)
Do đó
nên
(2)
Từ (1) và (2) suy ra
(đpcm)
c) Xét tam giác ABC và tam giác NMC có: ˆA=ˆN(=90 độ)
ˆC chung
Suy ra
Do đó
Xét tam giác BMC và tam giác ANC có: (cmt)
ˆC chung
Suy ra
Do đó hay .
Trong tam giác vuông ABC, ta có:
Từ đó suy ra (đpcm)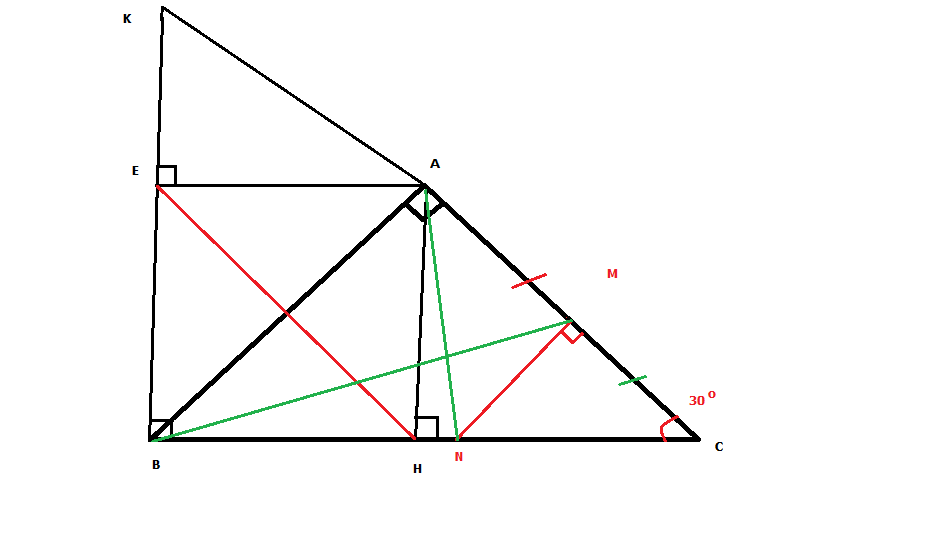
Chi tiết:
a) Xét tam giác ABC vuông tại A, số đo góc B là: Áp dụng tỉ số lượng giác trong tam giác vuông vào tam giác ABC, ta có: Suy ra
Áp dụng định lí Pythagore vào tam giác vuông, ta có:
= 24 (cm).
Vậy là ta đã có góc B, cạnh AC và cạnh BC.
b) Xét tứ giác AHBE có: (=90 độ) nên tứ giác AHBE là hình chữ nhật, suy ra AB = HE. (1)
Xét tam giác ABK và tam giác ACB có:
ˆBAK= ˆCAB(=90∘)
ˆAKB=ˆABC(cùng phụ với ˆC)
suy ra ΔABK đồng dạng ΔBCK(g.g)
Do đó
nên
(2)
Từ (1) và (2) suy ra
(đpcm)
c) Xét tam giác ABC và tam giác NMC có: ˆA=ˆN(=90 độ)
ˆC chung
Suy ra
Do đó
Xét tam giác BMC và tam giác ANC có: (cmt)
ˆC chung
Suy ra
Do đó hay .
Trong tam giác vuông ABC, ta có:
Từ đó suy ra (đpcm)

